 login/create account
login/create account
Let 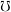 be a set,
be a set, 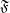 be the set of filters on
be the set of filters on 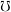 ordered reverse to set-theoretic inclusion,
ordered reverse to set-theoretic inclusion, 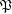 be the set of principal filters on
be the set of principal filters on 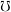 , let
, let  be an index set. Consider the filtrator
be an index set. Consider the filtrator 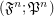 .
.
Conjecture If 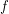 is a multifuncoid of the form
is a multifuncoid of the form 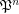 , then
, then 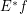 is a multifuncoid of the form
is a multifuncoid of the form 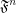 .
.
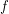 is a multifuncoid of the form
is a multifuncoid of the form 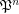 , then
, then 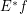 is a multifuncoid of the form
is a multifuncoid of the form 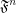 .
. See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
I found a really trivial proof of this conjecture. See this my draft article.
Definition A filtrator is a pair 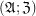 of a poset
of a poset  and its subset
and its subset 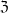 .
.
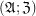 of a poset
of a poset  and its subset
and its subset 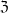 .
. Having fixed a filtrator, we define:
Definition 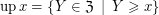 for every
for every 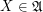 .
.
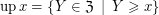 for every
for every 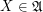 .
. Definition 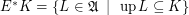 (upgrading the set
(upgrading the set 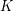 ) for every
) for every 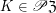 .
.
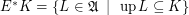 (upgrading the set
(upgrading the set 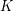 ) for every
) for every 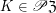 .
. Definition A free star on a join-semilattice  with least element 0 is a set
with least element 0 is a set  such that
such that 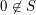 and
and ![\[ \forall A, B \in \mathfrak{A}: \left( A \cup B \in S \Leftrightarrow A \in S \vee B \in S \right) . \]](/files/tex/70420d16ddf609e4c505908182520a5bcf379d3e.png)
 with least element 0 is a set
with least element 0 is a set  such that
such that 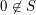 and
and ![\[ \forall A, B \in \mathfrak{A}: \left( A \cup B \in S \Leftrightarrow A \in S \vee B \in S \right) . \]](/files/tex/70420d16ddf609e4c505908182520a5bcf379d3e.png)
Definition Let  be a family of posets,
be a family of posets, 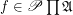 (
(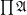 has the order of function space of posets),
has the order of function space of posets), 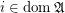 ,
, 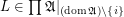 . Then
. Then ![\[ \left( \ensuremath{\operatorname{val}}f \right)_i L = \left\{ X \in \mathfrak{A}_i \hspace{0.5em} | \hspace{0.5em} L \cup \left\{ (i ; X) \right\} \in f \right\} . \]](/files/tex/402ce92b70bfd908eefa69f8ec7f3b5cd3cb72d2.png)
 be a family of posets,
be a family of posets, 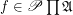 (
(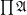 has the order of function space of posets),
has the order of function space of posets), 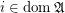 ,
, 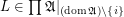 . Then
. Then ![\[ \left( \ensuremath{\operatorname{val}}f \right)_i L = \left\{ X \in \mathfrak{A}_i \hspace{0.5em} | \hspace{0.5em} L \cup \left\{ (i ; X) \right\} \in f \right\} . \]](/files/tex/402ce92b70bfd908eefa69f8ec7f3b5cd3cb72d2.png)
Definition Let  is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form
is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form  is an
is an 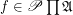 such that we have that:
such that we have that:
 is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form
is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form  is an
is an 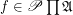 such that we have that:
such that we have that:- \item
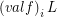 is a free star for every
is a free star for every 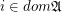 ,
, 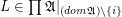 .
.
\item 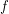 is an upper set.
is an upper set.
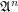 is a function space over a poset
is a function space over a poset  that is
that is 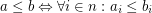 for
for 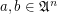 .
.
It is not hard to prove this conjecture for the case 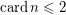 using the techniques from this my article. But I failed to prove it for
using the techniques from this my article. But I failed to prove it for 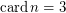 and above.
and above.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University