 login/create account
login/create account
Question For every  does there exists a
does there exists a  such that every graph with average degree smaller than
such that every graph with average degree smaller than  and girth at least
and girth at least  has a matching-cut?
has a matching-cut?
 does there exists a
does there exists a  such that every graph with average degree smaller than
such that every graph with average degree smaller than  and girth at least
and girth at least  has a matching-cut?
has a matching-cut? Let 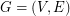 be a graph. A matching
be a graph. A matching  is a matching-cut if there exists a set
is a matching-cut if there exists a set  such that
such that 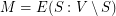 . Graphs having a matching-cut are called decomposable.
. Graphs having a matching-cut are called decomposable.
It is known that every graph with 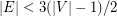 is decomposable [BFP11].
is decomposable [BFP11].
Bibliography
[C84] V. Chvátal, Recognizing decomposable graphs, J Graph Theory 8 (1984), 51–53
[BFP11] P. Bonsma, A. Farley, A. Proskurowski, Extremal graphs having no matching cuts, J Graph Theory (2011)
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University