 login/create account
login/create account
- \item Does
 hold over graphs of bounded tree-width? \item Is
hold over graphs of bounded tree-width? \item Is 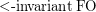 included in
included in 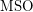 over graphs? \item Does
over graphs? \item Does 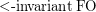 have a 0-1 law? \item Are properties of
have a 0-1 law? \item Are properties of 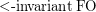 Hanf-local? \item Is there a logic (with an effective syntax) that captures
Hanf-local? \item Is there a logic (with an effective syntax) that captures 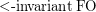 ?
? We describe the problem over finite vertex-colored graphs which we call graphs in the sequel. An ordered graph is a graph together with a linear order on its vertices. A property 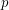 of ordered graphs is said to be order-invariant if it is independent of the linear order. I.e.
of ordered graphs is said to be order-invariant if it is independent of the linear order. I.e. 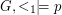 iff
iff 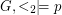 for all graphs
for all graphs  and all linear orders
and all linear orders  on
on  . Therefore, we now view an order-invariant property as a property over (unordered) graphs.
. Therefore, we now view an order-invariant property as a property over (unordered) graphs.
We denote by 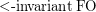 , the set of order-invariant first-order definable properties over graphs, where the first-order signature contains the vocabulary for graphs but also a linear order predicate. Note that it is undecidable whether a first-order query is order-invariant. In terms of expressive power, Gurevich showed that
, the set of order-invariant first-order definable properties over graphs, where the first-order signature contains the vocabulary for graphs but also a linear order predicate. Note that it is undecidable whether a first-order query is order-invariant. In terms of expressive power, Gurevich showed that 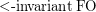 is strictly more expressive than
is strictly more expressive than 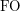 . However it is known that queries expressible in
. However it is known that queries expressible in 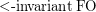 are Gaifman-local~[GS00]. It is also known that
are Gaifman-local~[GS00]. It is also known that 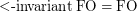 over finite trees~[BS09] (see also~[N05]).
over finite trees~[BS09] (see also~[N05]).
A glimpse beyond
One can view the linear order on top of the graph as a bijection between the vertices of the graph and an ordered prefix of the positive natural numbers. With this point of view, being order-invariant corresponds to being independent from the choice of the bijection. We could imagine allowing more predicates on the numerical side, and not just the linear order. Typically addition and multiplication. When both these predicates are present we denote by  the properties definable in first-order independently of the bijection. It was shown in~[AMSS10] that those properties are Gaifman local but with a polylog radius for the neighborhoods, and this polylog is tight. However the case when only addition is present is unclear. On top of all the questions above we could add:
the properties definable in first-order independently of the bijection. It was shown in~[AMSS10] that those properties are Gaifman local but with a polylog radius for the neighborhoods, and this polylog is tight. However the case when only addition is present is unclear. On top of all the questions above we could add:
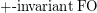 Gaifman-local?
Gaifman-local? The question of the inclusion of 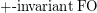 in
in 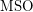 is already relevant over words:
is already relevant over words:
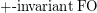 define non-regular languages over words?
define non-regular languages over words? See~[SS10] for more background about this question.
Bibliography
[AMSS10] Matthew Anderson, Dieter van Melkebeek, Nicole Schweikardt, and Luc Segoufin, Locality of queries definable in invariant first-order logic with arbitrary built-in predicates. In ICALP'11.
[BS09] Michael Benedikt and Luc Segoufin, Towards a characterization of order-invariant queries over tame graphs. J. Symb. Log. 74(1), 2009. Pages 168-186.
[GS00] Martin Grohe and Thomas Schwentick, Locality of order-invariant first-order formulas. ACM Trans. Comput. Log. 1(1), 2000. Pages 112-130.
[N05] Hannu Niemistö, On Locality and Uniform Reduction, LICS'05.
[SS10] Nicole Schweikardt and Luc Segoufin, Addition-Invariant FO and regularity, LICS'10.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University