login/create account
Conjecture Cross-composition product (for small indexed families of pointfree funcoids between posets with least elements) is a quasi-cartesian function (with injective aggregation) from the quasi-cartesian situation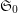 
of pointfree funcoids over posets with least elements to the quasi-cartesian situation 
of pointfree funcoids over posets with least elements.
of pointfree funcoids over posets with least elements 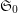to the quasi-cartesian situation of pointfree funcoids over posets with least elements. This conjecture is unsolved even for product of two multipliers.
A theorem little weaker than this conjecture was proved. So despite formally the conjecture isn't solved I mark it as solved, as the most important special case is considered.
See this article for a proof.
See Algebraic General Topology for definitions of used concepts.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University