Home ยป The robustness of the tensor product

The formal definition of robustness, and of the problem

On July 16th, 2007 ormeir says:

In all of the following definitions, the term "distance" refers to "relative Hamming distance".

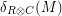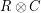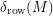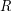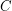Given a matrix $ M $, let $ \delta_{R \otimes C}(M) $ denote the distance from $ M $ to the nearest codeword of $ R \otimes C $. Let $ \delta_{\rm{row}}(M) $ denote the average distance of a row of $ M $ to $ R $, and let $ \delta_{\rm{col}}(M) $ denote the average distance of a column of $ M $ to $ C $. Finally, let 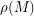$ \rho(M) $ denote the average of 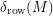$ \delta_{\rm{row}}(M) $ and $ \delta_{\rm{col}}(M) $.

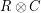The tensor product $ R \otimes C $ is said to be $ \alpha $-robust iff for every matrix $ M $ we have that $ \rho(M) \ge \alpha \cdot \delta_{R \otimes C}(M) $.

The question is, under what conditions the tensor product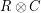 $ R \otimes C $ is $ \alpha $-robust for some constant $ \alpha $.

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options