 login/create account
login/create account
If the stability number is 1, that is if the digraph is a tournament, it follows Redei's Theorem stating that every tournament has a directed hamiltonian path. The conjecture has been proved by Havet [H] for digraphs having stability number 2.
The conjecture would give an easy inductive proof of Gallai-Roy Theorem: every digraph with chromatic number  contains a directed path on
contains a directed path on  vertices.
vertices.
Hahn and Jackson [HJ] conjectured that in contrast there is no directed path meeting every maximum stable set. In fact, they conjectured the following: For each positive integer  , there is a digraph
, there is a digraph  with stability number
with stability number  such that deleting the vertices of any
such that deleting the vertices of any 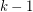 directed paths in
directed paths in  leaves a digraph with stability number
leaves a digraph with stability number  . This was proved by Fox and Sudakov [FS] by a probabilistic argument.
. This was proved by Fox and Sudakov [FS] by a probabilistic argument.
Bibliography
[FS] J. Fox and B. Sudakov, Paths and stability number in digraphs, Electronic Journal of Combiantorics, 16 (2009), no.1, N23.
[HJ] G. Hahn and B. Jackson, A note concerning paths and independence number in digraphs, Discrete Math. 82 (1990), 327–329.
[H] F. Havet. Stable set meeting every longest path. Discrete Mathematics, 289 (2004), no. 1-3, 169-173.
*[LPX] J.M. Laborde, C. Payan, and N.H. Xuong, Independent sets and longest directed paths in digraphs. In Graphs and other Combinatorial Topics (Prague, 1982)}, Teubner-Texte Math., Vol. 59 (1983), 173-177, Teubner, Leipzig.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University