 login/create account
login/create account
Conjecture Let  be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  , and let
, and let 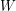 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 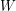 .
.
 be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  , and let
, and let 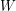 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 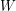 .
. Kotzig proved the converse statement:
Theorem Let  be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  and let
and let  be a decomposition into cycles of
be a decomposition into cycles of  . Then
. Then  admits an eulerian tour such that none of the
admits an eulerian tour such that none of the 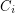 ,
, 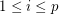 , contains two consecutive edges of
, contains two consecutive edges of 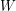 .
.
 be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  and let
and let  be a decomposition into cycles of
be a decomposition into cycles of  . Then
. Then  admits an eulerian tour such that none of the
admits an eulerian tour such that none of the 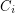 ,
, 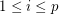 , contains two consecutive edges of
, contains two consecutive edges of 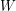 .
. For more details on eulerian graphs, see [F].
Bibliography
*[F] H. Fleischner. Eulerian Graphs and Related Topics. Part 1. Vol. 1. Annals of Discrete Mathematics, Vol. 45, (1990) North-Holland, Amsterdam.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University