Open Problem Garden

To switch a vertex of a simple graph is to exchange its sets of neighbours and non-neighbours. The graph so obtained is called a switching of the graph. The collection of switchings of a graph G is called the switching deck of . A graph is switching-reconstructible if every graph with the same deck as is isomorphic to .

There are four pairs of non-isomorphic graphs of order with the same switching deck. One of them consists of the empty graph and the -cycle.

Stanley [S] proved that a graph on vertices is switching-reconstructible if .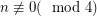

An analogous problem was posed for digraphs. Instead of complementing the edges at a vertex, one reverses each of its incident arc.