 login/create account
login/create account
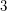 -uniform hypergraph on
-uniform hypergraph on  vertices which contains no complete
vertices which contains no complete 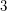 -uniform hypergraph on four vertices has at most
-uniform hypergraph on four vertices has at most 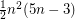 hyperedges.
hyperedges. 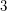 -uniform hypergraph on
-uniform hypergraph on  vertices which contains no complete
vertices which contains no complete 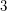 -uniform hypergraph on five vertices has at most
-uniform hypergraph on five vertices has at most 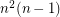 hyperedges.
hyperedges. Let 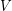 be an
be an  -set. A
-set. A  -uniform hypergraph
-uniform hypergraph 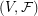 is complete if
is complete if 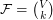 , the set of all
, the set of all 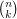
 -subsets of
-subsets of 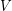 .
.
Let 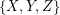 be a partition of
be a partition of 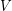 into three sets which are as nearly equal in size as possible, and let
into three sets which are as nearly equal in size as possible, and let 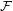 be the union of
be the union of 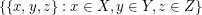 ,
, 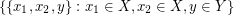 ,
, 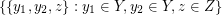 , and
, and 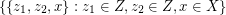 . This
. This 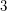 -uniform hypergraph has
-uniform hypergraph has 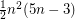 hyperedges and contains no complete
hyperedges and contains no complete 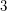 -uniform hypergraph on four vertices. Hence the first conjecture asserts that this hypergraph is extremal with this prpoerty.
-uniform hypergraph on four vertices. Hence the first conjecture asserts that this hypergraph is extremal with this prpoerty.
Let 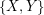 be a partition of
be a partition of 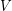 into two sets which are as nearly equal in size as possible, and let
into two sets which are as nearly equal in size as possible, and let 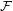 be the set of all
be the set of all 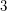 -subsets of
-subsets of 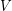 which intersect both
which intersect both 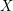 and
and 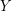 . This
. This 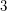 -uniform hypergraph has
-uniform hypergraph has 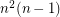 hyperedges and contains no complete
hyperedges and contains no complete 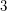 -uniform hypergraph on five vertices. Hence the second conjecture asserts that this hypergraph is extremal with this property.
-uniform hypergraph on five vertices. Hence the second conjecture asserts that this hypergraph is extremal with this property.
Bibliography
*[T] P. Turán, Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz. Lapok 48 (1941), 436--452.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University