Open Problem Garden

We say that two non-isomorphic graphs are cospectral if their adjacency matrices have the same spectrum (counted with multiplicity). A graph is spectrally determined if no other graphs are cospectral to it. It is unclear to me (M. DeVos) how to attribute this problem, but it was considered already in the 1950's and resonates with the famous problem "Can you hear the shape of a drum?" ([vDH]).

A priori, it might seem plausible for all graphs to be spectrally determined.. but this is false. The smallest counterexample is the cospectral pair given by 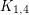and the graph obtained from 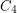by adding an isolated vertex. Some rich families of cospectral graphs are provided by strongly regular graphs, since any two strongly regular graphs with the same parameters will be cospectral.

For the special case of trees, Schwenk proved almost all trees are not spectrally determined. This was sharpened by Godsil and Mckay who showed that almost every tree has a cospectral graph 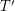so that in addition the complements of and 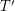are cospectral. Furthermore, an operation called Godsil-Mckay Switching defined by these authors gives a powerful tool to produce general graphs which are cospectral.

On the flip side, we seem to have a lack of good tools to prove that a given graph is spectrally determined.