 login/create account
login/create account
 matrix with different integer entries has two neighboring entries
matrix with different integer entries has two neighboring entries 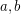 with
with  .
. Only neighbors in the same row or column are considered. Given a matrix  , let
, let 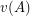 be the maximum difference between two neighboring entries of
be the maximum difference between two neighboring entries of  . Given integers
. Given integers 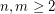 , let
, let 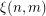 be the smallest possible value of
be the smallest possible value of 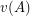 among all
among all 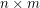 matrices
matrices  with different integer entries. Thus the conjecture asserts that
with different integer entries. Thus the conjecture asserts that 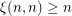 .
.
Consider the 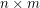 matrix
matrix 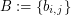 defined by
defined by 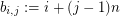 . The entries of
. The entries of  is
is ![$ [nm] $](/files/tex/f478f468fa3cce231f56c3c55aba9e7c854055e6.png) and
and 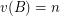 . Thus
. Thus  . Consequently the conjecture is equivalent to the assertion
. Consequently the conjecture is equivalent to the assertion 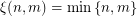 .
.
It can be easily seen that for any 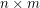 matrix
matrix  with different integer entries, there exists a matrix
with different integer entries, there exists a matrix 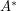 with the entries
with the entries ![$ [nm] $](/files/tex/f478f468fa3cce231f56c3c55aba9e7c854055e6.png) such that
such that 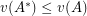 . Therefore, in the definition of
. Therefore, in the definition of 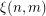 , we may assume that the entries of each matrix is
, we may assume that the entries of each matrix is ![$ [nm] $](/files/tex/f478f468fa3cce231f56c3c55aba9e7c854055e6.png) . Consequently the conjecture reduces to the case when the entries of the matrix is
. Consequently the conjecture reduces to the case when the entries of the matrix is ![$ [n^2] $](/files/tex/0a2e2b400ddc34a9d80ffb08094987e000785f51.png) .
.
I have proved the conjecture for  . The proof is separate for each of the 4 cases
. The proof is separate for each of the 4 cases  and pretty elementary. However, I am not so sure at the moment whether the conjecture is true for all
and pretty elementary. However, I am not so sure at the moment whether the conjecture is true for all  . If it turns out to be generally false, it would be an interesting problem to evaluate
. If it turns out to be generally false, it would be an interesting problem to evaluate 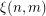 . I wonder if there are any related results.
. I wonder if there are any related results.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University