 login/create account
login/create account
Difference between neighbors in a matrix (Solved)
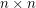 matrix with different integer entries has two neighboring entries
matrix with different integer entries has two neighboring entries 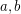 with
with 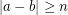 .
. Only neighbors in the same row or column are considered. Given a matrix  , let
, let 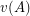 be the maximum difference between two neighboring entries of
be the maximum difference between two neighboring entries of  . Given integers
. Given integers 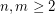 , let
, let 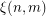 be the smallest possible value of
be the smallest possible value of 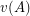 among all
among all 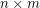 matrices
matrices  with different integer entries. Thus the conjecture asserts that
with different integer entries. Thus the conjecture asserts that 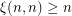 .
.
Consider the 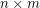 matrix
matrix 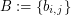 defined by
defined by 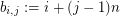 . The entries of
. The entries of 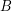 is
is ![$ [nm] $](/files/tex/f478f468fa3cce231f56c3c55aba9e7c854055e6.png) and
and 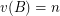 . Thus
. Thus 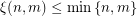 . Consequently the conjecture is equivalent to the assertion
. Consequently the conjecture is equivalent to the assertion 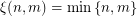 .
.
It can be easily seen that for any 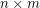 matrix
matrix  with different integer entries, there exists a matrix
with different integer entries, there exists a matrix 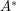 with the entries
with the entries ![$ [nm] $](/files/tex/f478f468fa3cce231f56c3c55aba9e7c854055e6.png) such that
such that 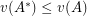 . Therefore, in the definition of
. Therefore, in the definition of 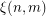 , we may assume that the entries of each matrix is
, we may assume that the entries of each matrix is ![$ [nm] $](/files/tex/f478f468fa3cce231f56c3c55aba9e7c854055e6.png) . Consequently the conjecture reduces to the case when the entries of the matrix is
. Consequently the conjecture reduces to the case when the entries of the matrix is ![$ [n^2] $](/files/tex/0a2e2b400ddc34a9d80ffb08094987e000785f51.png) .
.
I have proved the conjecture for 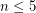 . The proof is separate for each of the 4 cases
. The proof is separate for each of the 4 cases 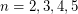 and pretty elementary. However, I am not so sure at the moment whether the conjecture is true for all
and pretty elementary. However, I am not so sure at the moment whether the conjecture is true for all 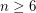 . If it turns out to be generally false, it would be an interesting problem to evaluate
. If it turns out to be generally false, it would be an interesting problem to evaluate 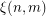 . I wonder if there are any related results.
. I wonder if there are any related results.
Bibliography
* indicates original appearance(s) of problem.
Related questions
Dear Daniel, thank you for the very nice proof! Theorem 11 from the lecture notes you refer to suggests some answers to other general questions related to the conjecture (let us now refer to it as Theorem 0). In particular I have the following 2 questions in mind.
1. I wonder how the generalization of Theorem 0 to higher dimensional matrices looks like. More specifically, given integers 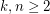 , what is the smallest value, denoted
, what is the smallest value, denoted 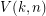 , of
, of 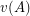 among all
among all ![$ [k]^n $](/files/tex/2b7d2c8c7995ee0622330e8af48a18f578ee7ebc.png) -matrices
-matrices  with distinct integer entries? Theorem 0 states that
with distinct integer entries? Theorem 0 states that 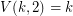 . Theorem 11 implies that
. Theorem 11 implies that 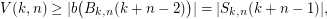 where
where ![$ B_{k,n}(r):=\{x\in[k]^n : |x| \le r\} $](/files/tex/65beeb7dfef6b4f8c24171d57526bda6ffada536.png) and
and ![$ S_{k,n}(r):=\{x\in[k]^n : |x| = r\} $](/files/tex/68c4d6db4a884ab1ad555d28cfb1dd7597bd45e3.png) . My feeling is that
. My feeling is that 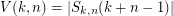 . What do you think? Note that
. What do you think? Note that 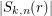 is the number of all ordered partitions of
is the number of all ordered partitions of  into exactly
into exactly  parts not exceeding
parts not exceeding  .
.
bandwidth
Dear Dr. Lioubimov!
At first sight your feeling seemed plausible, but since then i managed to find the more general problem: The graph bandwidth problem. (see wiki page)
At the wikipedia page, you can see that a classical result of Harper is the bandwidth of the hypercube. Well, if your feeling were true, the bandwidth of the cube would be the middle binomial coefficient, which is not true.
We can see this in a different way too, i'll give some heuristics. Take a look at the proof of the 2 dimensional case: We had a single vertex which had a big label (at least n(n-1)/2+n). And we concluded that since it has at least one vertex with "small" label, we found a big difference. If we only have 2 dimensions, this bound is sharp, because the degrees of the vertices are not too big. In higher dimensionan grids there are more neighbours of this vertex with "small" labell. Thus a better lower bound can be obtained.
Sincerely, Daniel Soltész
Solution
Dear Dr. Lioubimov
Your problem is equivalent to the following: We label the vertces of the nxn grid graph with distinct elements from the set [n^2]. Then there are adjacent vertices such that their labels differ by at least n. I think i found a solution. The key related result is the vertex isoperimetric inequality in the grid. For our problem it is enough to consider the corollary 12 in the following .pdf:
https://www.dpmms.cam.ac.uk/~par31/notes/extcomb.pdf
With parameters: n=2 since we are in a 2 dimensional grid. Let A be the set which have the labels: 1,2,..., n(n-1)/2. Clearly then we can set r=n-1 and with t=1 we obtain that there are at least n neighbors of this set. This finishes our proof since one of these neighbors will have a label of at least n(n-1)/2+n.
Sincerely Daniel Soltész

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Related questions: continued
2. What is the smallest number, denoted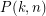 , to guarantee that a
, to guarantee that a ![$ [k]^n $](/files/tex/2b7d2c8c7995ee0622330e8af48a18f578ee7ebc.png) -matrix
-matrix  with the entries
with the entries ![$ [k^n] $](/files/tex/4b7fd2697422fa70e52892429fa1ce7451c795a6.png) has 2 neighboring entries
has 2 neighboring entries 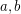 such that
such that 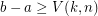 and
and 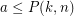 ? Obviously,
? Obviously, 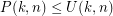 , where
, where 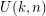 is the smallest number such that any subset of
is the smallest number such that any subset of ![$ [k]^n $](/files/tex/2b7d2c8c7995ee0622330e8af48a18f578ee7ebc.png) of size
of size 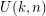 has at least
has at least 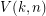 neighbors. Due to Theorem 11,
neighbors. Due to Theorem 11, 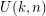 is the smallest number
is the smallest number  such that the initial segment
such that the initial segment 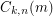 of length
of length  in the simplicial order on
in the simplicial order on ![$ [k]^n $](/files/tex/2b7d2c8c7995ee0622330e8af48a18f578ee7ebc.png) has
has 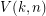 neighbors. In your proof you used the fact that
neighbors. In your proof you used the fact that 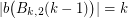 , which implies by Theorem 11 that
, which implies by Theorem 11 that 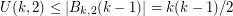 . However this bound is not tight. Consider the hamming ball
. However this bound is not tight. Consider the hamming ball 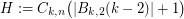 . It is easy to see that
. It is easy to see that 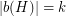 and
and 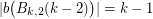 . Thus
. Thus 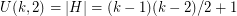 . What about higher dimensions?
. What about higher dimensions?