Home ยป Difference between neighbors in a matrix

Related questions

On July 6th, 2013 Vadim Lioubimov says:

Dear Daniel, thank you for the very nice proof! Theorem 11 from the lecture notes you refer to suggests some answers to other general questions related to the conjecture (let us now refer to it as Theorem 0). In particular I have the following 2 questions in mind.

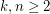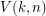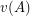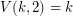1. I wonder how the generalization of Theorem 0 to higher dimensional matrices looks like. More specifically, given integers $ k,n\ge2 $, what is the smallest value, denoted $ V(k,n) $, of $ v(A) $ among all $ [k]^n $-matrices $ A $ with distinct integer entries? Theorem 0 states that $ V(k,2)= k $. Theorem 11 implies that 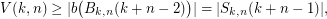$$ V(k,n)\ge |b\big( B_{k,n}(k+n-2)\big)| = |S_{k,n}(k+n-1)|, $$ where $ B_{k,n}(r):=\{x\in[k]^n : |x| \le r\} $ and $ S_{k,n}(r):=\{x\in[k]^n : |x| = r\} $. 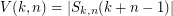My feeling is that $ V(k,n)= |S_{k,n}(k+n-1)| $. What do you think? Note that 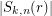$ |S_{k,n}(r)| $ is the number of all ordered partitions of $ r $ into exactly $ n $ parts not exceeding $ k $.

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options