 login/create account
login/create account
Problem (1) Prove that there exist infinitely many positive integers  such that
such that 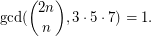
 such that
such that 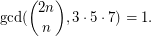
Problem (2) Prove that there exists only a finite number of positive integers  such that
such that 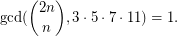
 such that
such that 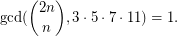
The binomial coefficient 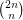 is not divisible by prime
is not divisible by prime 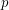 iff all the base-
iff all the base-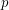 digits of
digits of  are smaller than
are smaller than 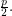
It has been conjectured that 1, 2, 10, 3159, and 3160 are the only positive numbers for which 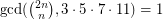 holds.
holds.
Bibliography
Sequence A030979: Numbers n such that C(2n,n) is not divisible by 3, 5 or 7.
Andrew Granville. "The Arithmetic Properties of Binomial Coefficients."
* indicates original appearance(s) of problem.

 ." Math. Comp. 29 (1975), 83-92.
." Math. Comp. 29 (1975), 83-92. Drupal
Drupal CSI of Charles University
CSI of Charles University