 login/create account
login/create account
Divisibility of central binomial coefficients
 such that
such that 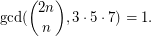
 such that
such that 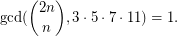
The binomial coefficient 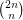 is not divisible by prime
is not divisible by prime 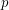 iff all the base-
iff all the base-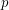 digits of
digits of  are smaller than
are smaller than 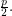
It has been conjectured that 1, 2, 10, 3159, and 3160 are the only positive numbers for which 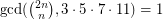 holds.
holds.
Bibliography
Sequence A030979: Numbers n such that C(2n,n) is not divisible by 3, 5 or 7.
Andrew Granville. "The Arithmetic Properties of Binomial Coefficients."
* indicates original appearance(s) of problem.
2, 10, and 3159 are not valid for problem (2)
In the initial comment five values are stated to be not divisible by 3, 5, 7, and 11. That is true for 1 and 3160 but not for 2, 10, and 3159:
The last base-3-digit of 2 is 2. The last base-11-digit of 10 is 10. The last base-5-digit 3159 is 4.
Or check these facts:
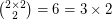

2 and 3159 are not in the sequence A030979 (mentioned in the bibliography).
Reference for problem (2)
It appears that the right reference for question 2 should be A151750 instead.
Problem 1 solved?
Looks like Problem 1 was solved by http://arxiv.org/PS_cache/arxiv/pdf/1010/1010.3070v1.pdf

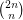 ." Math. Comp. 29 (1975), 83-92.
." Math. Comp. 29 (1975), 83-92. Drupal
Drupal CSI of Charles University
CSI of Charles University
It seems Problem (1) was
It seems Problem (1) was solved last year, see http://arxiv.org/abs/1010.3070
How about Problem 2?