 login/create account
login/create account
Conjecture Every monovalued reloid is metamonovalued.
Let  is a monovalued reloid. Then there is a principal filter
is a monovalued reloid. Then there is a principal filter 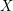 and principal monovalued reloid
and principal monovalued reloid 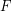 such that
such that  .
.
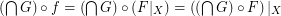
It follows that it's enough to prove it for monovalued principal reloids.
Bibliography
Solved in the new version of this book preprint: *Algebraic General Toplogy. Volume 1
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University