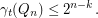The conjecture is false and it can be seen that this is so by using a computer program. For example which is not a power of two.
Alternatively we can argue as follows. For any graph we clearly have Now the bound by Alon and Spencer states In particular this implies that for any constant and large enough we have
login/create account
Drupal
CSI of Charles University
The conjecture is false
The conjecture is false and it can be seen that this is so by using a computer program. For example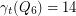
which is not a power of two.
Alternatively we can argue as follows. For any graph
we clearly have 
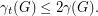Now the bound by Alon and Spencer states 
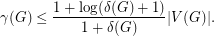In particular this implies that for any constant 
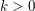and large enough 
we have 