 login/create account
login/create account
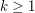 and
and 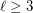 , there is an integer
, there is an integer 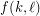 such that for every set
such that for every set 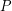 of at least
of at least 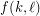 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:- \item
 contains
contains  collinear points, or \item
collinear points, or \item 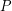 contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour)
contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour) This conjecture is trivially true for 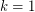 with
with 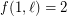 , and for
, and for 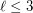 and
and 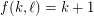 . The Motzkin-Rabin Theorem [PS] says that the conjecture is true for
. The Motzkin-Rabin Theorem [PS] says that the conjecture is true for 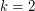 with
with 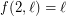 . The conjecture is related to the Hales-Jewett Theorem, which states that for sufficiently large
. The conjecture is related to the Hales-Jewett Theorem, which states that for sufficiently large 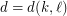 , every
, every  -colouring of the
-colouring of the  -dimensional grid
-dimensional grid 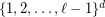 contains a monochromatic "combinatorial"' line of
contains a monochromatic "combinatorial"' line of 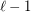 points. Say the Geometric Hales-Jewett Theorem is the statement obtained by replacing "combinatorial line" by "geometric line" (that is, a set of collinear points). This theorem is discussed in [P]. The conjecture is a generalisation of the Geometric Hales-Jewett Theorem.
points. Say the Geometric Hales-Jewett Theorem is the statement obtained by replacing "combinatorial line" by "geometric line" (that is, a set of collinear points). This theorem is discussed in [P]. The conjecture is a generalisation of the Geometric Hales-Jewett Theorem.
This conjecture was disproved by Vytautas Gruslys [G].
Bibliography
[P] D.H.J. Polymath. Density Hales-Jewett and Moser numbers, arXiv:1002.0374, 2010.
*[PW] Attila Pór and David R. Wood. On visibility and blockers, J. Computational Geometry 1:29-40, 2010.
[PS] Lou M. Pretorius and Konrad J. Swanepoel. An Algorithmic Proof of the Motzkin-Rabin Theorem on Monochrome Lines, The American Mathematical Monthly 111.3:245-251, 2004.
[G] Vytautas Gruslys. A counterexample to a geometric Hales-Jewett type conjecture. J. Comput. Geom. 5.1:245-249, 2014.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University