 login/create account
login/create account
Problem Let  and
and 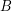 be infinite sets. Characterize the set of all coatoms of the lattice
be infinite sets. Characterize the set of all coatoms of the lattice 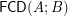 of funcoids from
of funcoids from  to
to 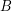 . Particularly, is this set empty? Is
. Particularly, is this set empty? Is 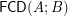 a coatomic lattice? coatomistic lattice?
a coatomic lattice? coatomistic lattice?
 and
and 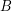 be infinite sets. Characterize the set of all coatoms of the lattice
be infinite sets. Characterize the set of all coatoms of the lattice 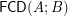 of funcoids from
of funcoids from  to
to 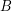 . Particularly, is this set empty? Is
. Particularly, is this set empty? Is 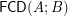 a coatomic lattice? coatomistic lattice?
a coatomic lattice? coatomistic lattice? See Algebraic General Topology for definitions of used concepts.
Solved:
Coatoms of 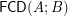 are principal funcoids corresponding to binary relations of the form
are principal funcoids corresponding to binary relations of the form 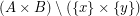 where
where 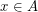 ,
, 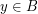 .
.
The set of funcoids is atomic but not atomistic.
See new version of the book Algebraic General Topology.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University