 login/create account
login/create account
 has a decomposition into a spanning tree, a family of cycles and a matching.
has a decomposition into a spanning tree, a family of cycles and a matching. We state the conjecture in a more precise manner:
Let  be a connected cubic graph. Then
be a connected cubic graph. Then  contains a spanning tree
contains a spanning tree 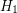 , a
, a 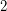 -regular subgraph
-regular subgraph 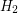 and a matching
and a matching 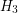 (where only
(where only 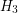 and not
and not 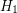 or
or 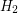 may be empty) such that
may be empty) such that 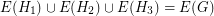 and
and 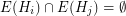 for every
for every 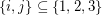 with
with 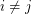 .
.
The conjecture holds for all hamiltionian cubic graphs and for all connected planar cubic graphs, see [1] and see also [7].
Every cubic graph G which has a spanning tree T such that every vertex of T has degree three or one (such spanning tree T is called a HIST) obviously satisfies this conjecture. But not every connected cubic graph has a HIST, see [2].
The 3-Decomposition Conjecture has been shown to be equivalent to the following conjecture:
 be connected graph where every vertex has degree two or three. Suppose that for every cycle
be connected graph where every vertex has degree two or three. Suppose that for every cycle 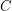 of
of  ,
, 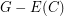 is disconnected, then
is disconnected, then  has a decomposition into a spanning tree
has a decomposition into a spanning tree  and a matching
and a matching 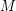 , i.e
, i.e 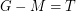 .
. Note that every cycle 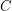 which passes through a vertex of degree two satisfies the condition that G-E(C) is disconnected.
which passes through a vertex of degree two satisfies the condition that G-E(C) is disconnected.
Remark: The 3-Decomposition Conjecture has also been shown to hold for other classes of cubic graphs, see for instance [3,4]. A survey on the 3-Decompostion conjecture has been given by the author 2015 in Pilsen (at that time the planar case was still open) see iti.zcu.cz/plzen15/talks/1-2a-Arthur-Survey_decomposition.ppt (and press play if you find the play button). Note that there are several papers on the problem whether a planar graph  has a matching
has a matching 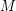 such that
such that 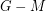 is acyclic, see for instance [6].
is acyclic, see for instance [6].
Bibliography
[1] Arthur Hoffmann-Ostenhof, Tomáš Kaiser, Kenta Ozeki, \arXiv[Decomposing planar cubic graphs] 1609.05059 [math.CO]
[2] Arthur Hoffmann-Ostenhof, Kenta Ozeki, \arXiv[On HISTs in Cubic Graphs] 1507.07689 [math.CO]
[3] F. Abdolhosseini, S. Akbari, H. Hashemi, M.S. Moradian, \arXiv[Hoffmann-Ostenhof's conjecture for traceable cubic graphs] 1607.04768[math.CO]
[4] Anna Bachstein, Dong Ye (talk): www.rwoodroofe.math.msstate.edu/workshop2014/bachstein_slides.pdf
[5] Arthur Hoffmann-Ostenhof (talk): www.iti.zcu.cz/plzen15/talks/1-2a-Arthur-Survey_decomposition.ppt
[6] Yingqian Wang, Qijun Zhang, Discrete Mathematics 311 (2011) 844–849, Decomposing a planar graph with girth at least 8 into a forest and a matching
[7] Kenta Ozeki, Dong Ye, Decomposing plane cubic graphs, European Journal of Combinatorics 52 (2016) 40-46.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University