 login/create account
login/create account
Let  be a graph and
be a graph and 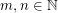 . The graph
. The graph 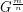 is defined to be the
is defined to be the  -power of the
-power of the  -subdivision of
-subdivision of  . In other words,
. In other words, 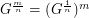 .
.
 be a graph with
be a graph with 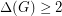 . Then
. Then 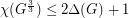 .
. Bibliography
[1] Mahsa Mozafari-Nia and M. N. Iradmusa, Simultaneous coloring of vertices and incidences of graphs, Australasian Journal of Combinatorics, Vol. 85, Mo. 3, pp. 287-307, 2023.
[2] Mahsa Mozafari-Nia and M. N. Iradmusa, Simultaneous coloring of vertices and incidences of outerplanar graphs, Electronic Journal of Graph Theory and Applications, Vol.11, No.1, pp.245-262, 2023.
[3] Mahsa Mozafari-Nia and M. N. Iradmusa, A note on coloring of 3/3-power of subquartic graphs, Australasian Journal of Combinatorics, Vol. 79, No. 3, pp. 454-460, 2021.
[4] M. N. Iradmusa, A short proof of 7-colorability of 3/3-power of subcubic graphs, Iranian Journal of Science and Technology, Transactions A: Science, Vol. 44, No. 1, pp. 225-226, 2020.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University