Home » Subject » Geometry » Polytopes
Importance: Medium ✭✭
Author(s): Deza, Antoine
Terlaky, Tamas
Zinchenko, Yuriy
Subject: Geometry
» Polytopes
Keywords: curvature
polytope
Recomm. for undergrads: no
Posted by: deza
on: September 30th, 2007
Conjecture   The order of the largest total curvature of the primal central path over all polytopes defined by $ n $ inequalities in dimension $ d $ is $ n $.

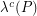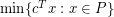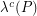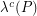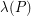Let $ \lambda^c(P) $ denote the total curvature of the central path corresponding to the linear optimization problem $ \min \{ c^Tx : x\in P\} $. The quantity $ \lambda^c(P) $ can be regarded as the continuous analogue of the edge-length of the shortest path between a pair of vertices. Considering the largest $ \lambda^c(P) $ over all possible $ c $ we obtain the quantity $ \lambda(P) $, referred to as the curvature of a polytope. Following the analogy with the diameter, let 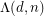$ \Lambda(d,n) $ be the largest total curvature 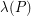$ \lambda(P) $ of the primal central path over all polytopes 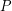$ P $ defined by $ n $ inequalities in dimension $ d $.

Holt and Klee~[HK] showed that, for 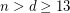$ n> d\geq 13 $, the conjecture of Hirsch is tight. We have the following continuous analogue of the result of Holt and Klee:

[DTZa] 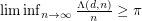$ \liminf_{n\rightarrow\infty}\frac{\Lambda(d,n)}{n}\geq \pi $, that is, 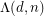$ \Lambda(d,n) $ is bounded below by a constant times $ n $.

The special case of 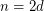$ n=2d $ of the conjecture of Hirsch is known as the $ d $-step conjecture, and it has been shown by Klee and Walkup~[KW] that the $ d $-step conjecture is equivalent to the Hirsch conjecture. We have the following continuous analogue of the result of Klee and Walkup:

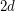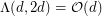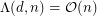[DTZb] If the order of the curvature is less than the dimension $ d $ for all polytope defined by $ 2d $ inequalities and for all $ d $, then the order of the curvature is less that the number of inequalities for all polytopes; that is, if $ \Lambda(d,2d)=\mathcal{O}(d) $ for all $ d $, then $ \Lambda(d,n)=\mathcal{O}(n) $.

Bibliography

[DMS] J.-P. Dedieu, G. Malajovich and M. Shub: On the curvature of the central path of linear programming

*[DTZa] A. Deza, T. Terlaky and Y. Zinchenko: Polytopes and arrangements : diameter and curvature. Operations Research Letters (to appear).

[DTZb] A. Deza, T. Terlaky and Y. Zinchenko: The continuous d-step conjecture for polytopes. AdvOL-Report 2007/16, McMaster University (2007).

[HK] F. Holt and V. Klee: Many polytopes meeting the conjectured Hirsch bound. Discrete and Computational Geometry 20 (1998) 1--17.

[KW] V. Klee and D. Walkup: The $ d $-step conjecture for polyhedra of dimension $ d<6 $. Acta Mathematica 133 (1967) 53--78.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options