 login/create account
login/create account
Question Is it true that every permutation of positive integers must contain monotone 4-term arithmetic progressions?
It is not difficult to see that any permutation of positive integers contains a monotone 3-term arithmetic progression, i.e., that for any permutation 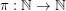 there is a 3-term arithmetic progression
there is a 3-term arithmetic progression 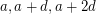 such that
such that 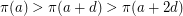 or
or 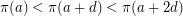 .
.
In [DEGS] an example of a permutation of 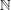 that does not contain a monotone 5-term arithmetic progression is given.
that does not contain a monotone 5-term arithmetic progression is given.
Bibliography
*[DEGS] J. A. Davis, R. C. Entringer, R. L. Graham, and G. J. Simmons, On permutations containing no long arithmetic progression, Acta Arithmetica XXXIV.1 (1977), 81-90.
[LR] Bruce M. Landman and Aaron Robertson, Ramsey Theory on the Integers, Stud. Math. Libr. 24, AMS Providence, RI, 2004.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University