 login/create account
login/create account
 is a highly arc transitive digraph with two ends, then every tile of
is a highly arc transitive digraph with two ends, then every tile of  is a disjoint union of complete bipartite graphs.
is a disjoint union of complete bipartite graphs. It follows from a theorem of Dunwoody [D] that every vertex transitive graph  with two ends has a system of imprimitivity
with two ends has a system of imprimitivity 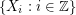 with finite blocks so that the cyclic order
with finite blocks so that the cyclic order 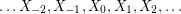 is preserved by the automorphism group (of
is preserved by the automorphism group (of  ). If
). If  is edge-transitive, then every edge of
is edge-transitive, then every edge of  must have its ends in two consecutive blocks, so in this case
must have its ends in two consecutive blocks, so in this case  is an edge-disjoint union of the (isomorphic) bipartite graphs
is an edge-disjoint union of the (isomorphic) bipartite graphs ![$ G[X_i,X_{i+1}] $](/files/tex/d6b7152ef06477fc272ef03a234493014768c7b0.png) for
for 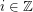 - which we shall call tiles. Note that the tiles are edge-transitive.
- which we shall call tiles. Note that the tiles are edge-transitive.
This gives us a good description of edge-transitive graphs with two ends; each is made up by gluing together copies of a tile in a linear order. If  is a 2-arc transitive digraph with two ends, then all edges in each tile must be oriented consistently, so by possibly reordering, we may assume that every edge in
is a 2-arc transitive digraph with two ends, then all edges in each tile must be oriented consistently, so by possibly reordering, we may assume that every edge in ![$ G[X_i,X_{i+1}] $](/files/tex/d6b7152ef06477fc272ef03a234493014768c7b0.png) is oriented from
is oriented from 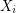 to
to 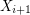 . The above conjecture asserts that under the added symmetry condition of high arc transitivity, each tile has a simple structure - namely it is a union of (consistently oriented) complete bipartite graphs.
. The above conjecture asserts that under the added symmetry condition of high arc transitivity, each tile has a simple structure - namely it is a union of (consistently oriented) complete bipartite graphs.
It is easy to construct a highly arc transitive two ended graph by simply using the complete bipartite graph 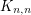 (with all edges oriented consistently) as a tile. Mckay and Praeger found the following pretty construction of a highly arc transitive digraph with tiles isomorphic to a disjoint union of complete bipartite graphs: Let
(with all edges oriented consistently) as a tile. Mckay and Praeger found the following pretty construction of a highly arc transitive digraph with tiles isomorphic to a disjoint union of complete bipartite graphs: Let  be a finite set, let
be a finite set, let  be a positive integer, and define
be a positive integer, and define  to be the digraph with vertex set
to be the digraph with vertex set 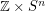 and an edge from
and an edge from 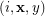 to
to 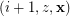 if
if 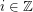 ,
, 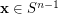 , and
, and 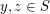 . A generalized (twisted) version of this construction was introduced by Cameron, Praeger, and Wormald [CPW], but again, every tile in this construction is a disjoint unions of bipartite graphs, and it looks hard to do anything else.
. A generalized (twisted) version of this construction was introduced by Cameron, Praeger, and Wormald [CPW], but again, every tile in this construction is a disjoint unions of bipartite graphs, and it looks hard to do anything else.
Bibliography
*[CPW] P. J. Cameron, C. E. Praeger, and N. C. Wormald, Infinite highly arc transitive digraphs and universal covering digraphs. Combinatorica 13 (1993), no. 4, 377--396. MathSciNet.
[D] M. J. Dunwoody, Cutting up graphs. Combinatorica 2 (1982), no. 1, 15--23. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University