 login/create account
login/create account
Conjecture Does every Jordan curve have 4 points on it which form the vertices of a square?
A Jordan curve is a continuous function  from the closed interval
from the closed interval ![$ [0,1] $](/files/tex/f65c588a56e7eca31976481db4eeeae4e72a4d3a.png) to the plane
to the plane 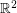 with the properties that
with the properties that  is injective on the half-open interval
is injective on the half-open interval 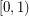 (i.e.,
(i.e.,  is simple) and
is simple) and 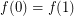 (i.e.,
(i.e.,  is closed).
is closed).
Bibliography
[M] Meyerson, M.D., Equilateral triangles and continuous curves, Fund. Math. 110, (1980), 1--9.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University