 login/create account
login/create account
3-accessibility of Fibonacci numbers
A set 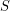 is
is  -accessible if for any
-accessible if for any  -coloring of
-coloring of 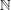 ,
, 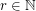 , there exist long monochromatic
, there exist long monochromatic 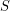 -diffsequences, i.e., for any
-diffsequences, i.e., for any 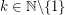 there is a monochromatic sequence
there is a monochromatic sequence 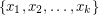 such that
such that 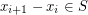 , for all
, for all 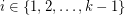 .
.
The set of Fibonacci numbers 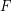 is 2-accessible. [LR1]
is 2-accessible. [LR1]
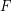 is not 6-accessible. [AGJL]
is not 6-accessible. [AGJL]
It is known that a 3-coloring of any 27 consecutive positive integers yields a monochromatic 4-term 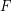 -diffsequence.
-diffsequence.
Bibliography
[AGJL] Hayri Ardal, David Gunderson, Veselin Jungi\'c, and Bruce Landman, {\it On Accessibility of the Set of Fibonacci Numbers}, In Preparation
*[LR1] Bruce M. Landman and Aaron Robertson, {\it Avoiding Monochromatic Sequences With special Gaps}, SIAM J. Discrete Math Vol. 21 (2007), no. 3, 794--801.
[LR2] Bruce M. Landman and Aaron Robertson, Ramsey Theory on the Integers, Stud. Math. Libr. 24, AMS Providence, RI, 2004
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University