 login/create account
login/create account
Square achievement game on an n x n grid
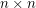 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15. Bibliography
R. Bacher and S. Eliahou, "Extremal binary matrices without constant 2-squares," J. of Combinatorics, Volume 1, Number 1, 77-100, 2010.
* Erickson, Martin, "Pearls of Discrete Mathematics," CRC Press, 2010
* indicates original appearance(s) of problem.
This is not mathematics
I suspect this problem can be solved only with brute force for every particular n and is not a nice mathematical conjecture (just like the question who wins in chess, white or black, playing both with the optimal strategy).
-- Victor Porton - http://www.mathematics21.org
On drawn games for n up to 14
I should have read the referenced article by Bacher and Eliahou before trying to find drawn games. But I've read it now.
Among many other things, the authors describe parametric families of square-free configurations for n=14.
Not all of those configurations do provide the required relation of the numbers of symbols of both sorts needed to be an end-configuration of the game.
But one can, for example, take the family A1, give the variables x1 up to x8 the value 0 (or O, resp.) and the variables x9 up to x16 the value 1 (or X, resp.).
Then the numbers of symbols of both sorts are equal and that square-free configuration is also a correct end-configuration of the game for n=14.
An URL of the technical report version of the referenced article
http://www-lmpa.univ-littoral.fr/publications/articles/lmpa404.pdf
Drawn game for n=12
I've had not much hope to find one in an acceptable time but after running another couple of hours my program delivered this square-free end-configuration for n=12:
oooooooxxxox
xoxoxoxoxoxx
xoxxooxooxxo
oooxxxooxxoo
oxooxoxxxoxo
xxxooxoxoxox
xoxxxxooooxx
oxoxoxxoxoox
ooxoooxxoxox
xxooxooxoxxo
oooxoxoxooxx
xoxxxoxxxoox
Drawn games for grid sizes from 3 to 11
Running a self-written program I've found the square-less end-configurations to be listed (because of the 1000 characters limit) in a comment of this comment for the grid sizes (n) from 3 to 11.
If I understand the note in the problem text right, this proofs that there is no sure winning strategy for those sizes.
On my 1 GHz Celeron/PIII the search for n=11 took 65 seconds.
But I gave up the search for n=12 after circa 12 hours of calculation estimating the 130-fold duration for the complete search. On the other side: In the first 8 hours there was a square-less configuration just before the occupation of the last field.
I withdraw the conclusion
The note in the problem text let me assume that it is proven that if the game for some grid size n must have a winner there is a sure winning strategy for the first player.
Taking in account that implication only, one cannot, as I did, conclude that there is no sure winning strategy if a game could be drawn.
Text corrections
It should stand 'proves' instead of 'proofs' and 'square-free' instead of 'square-less'.
A list of square-free end-configurations for n from 3 to 11
3
ooo
oxo
xxx
4
oooo
oxox
xoxx
xxxo
5
ooooo
oxoxo
ooxxo
xoxox
xxxxx
6
oooooo
oxoxox
ooxxoo
xoxoxx
xxxxox
xooxxx
7
ooooooo
oxoxoxo
ooxxoox
xxooxxx
oxoxxox
xxxooox
xoxxxxo
8
oooooooo
oxoxoxox
ooxxooxx
xxooxxxo
oxoxxoxx
xxxoxoox
xoxoxxox
xooooxxx
9
ooooooooo
oxoxoxoxo
ooxxooxxo
xoooxxxoo
oxoxxoxxx
xxxoxooox
xoxoxxoxx
xxoxoxoox
oxxxoxxox
10
ooooooooox
oxoxoxoxoo
oxxooxxxxo
ooxxxoxoxo
oxooxoxxoo
xxxooooxxx
xoxoxxoxox
xooxoxxoxx
xxoxxoxoox
xoxxooxxox
11
oooooooooxx
oxoxoxxoxox
oxxoxxooxox
ooxxxooxxoo
oxooxoxxoox
xxxxoooooxx
xoxooxoxxxo
xooxoxxoxoo
xxooxxoooxo
xoxxxooxoxx
xoxoxoxxxxo

 Drupal
Drupal CSI of Charles University
CSI of Charles University
A new reference
My new article "Guaranteed successful strategies for a square achievement game on an n by n grid" concerning that problem is now accessible via http://arxiv.org/abs/1109.2341 .