login/create account
Algebraic independence of pi and e
and 
are Bibliography
* indicates original appearance(s) of problem.
in which subfield K of which field L?
On February 16th, 2011 Comet says:
After all, e to the pi i = -1, so this shows that pi and e are not always algebraically independent.
By definition?
On July 16th, 2011 Anonymous says:
I think any two distinct transcendental numbers must be algebraically independent, almost by definition. Since e and pi are transcendental, they must be a. i. No? - David Spector
not all transcedentials are algebraically independant
On August 5th, 2011 cubola zaruka says:
pi and 4-pi are both transcedential and sum to 4, so are not algebraically independant.
two transcendentals are not necessarily algebraically independen
On July 21st, 2011 Anonymous says:
e and e^2 are both transcendental but (e,e^2) makes the two-variable polynomial f(x,y)=x^2-y equal to zero
Drupal
CSI of Charles University
Schanuel's conjecture
Assuming Schanuel's conjecture, one can show that
and 
are algebraically independent over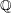 
.