 login/create account
login/create account
¿Are critical k-forests tight?
Let  be a
be a  -uniform hypergraph. If
-uniform hypergraph. If  is a critical
is a critical  -forest, then it is a
-forest, then it is a  -tree.
-tree.
We say that a hypergraph 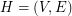 is a
is a  -graph if it is
-graph if it is  -uniform, and denote its order by
-uniform, and denote its order by 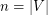 and its size by
and its size by  .
.
Laszlo Lovasz introduced the following concept: a  -graph
-graph 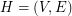 is said to be a
is said to be a  -forest if for every edge
-forest if for every edge  there exists a
there exists a  -colouing
-colouing ![$ \varsigma\colon V\to[k] $](/files/tex/cf5fbfa8b5817a2631ce388b4cbef4ddb3472a8a.png) such that
such that ![$ \varsigma(e')=[k]\Leftrightarrow e'=e $](/files/tex/959d782cabecb10abd1cd24a41e6a0a70d2970fc.png) ; that is, such that only the edge
; that is, such that only the edge  receives the
receives the  colours in its vertices. Clearly a
colours in its vertices. Clearly a 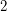 -forest is simply a forest in the usual sense (i.e., an acyclic graph). Lovasz proved that
-forest is simply a forest in the usual sense (i.e., an acyclic graph). Lovasz proved that
 -forest has size at most
-forest has size at most 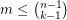 .
. On the other hand, Victor Neumann-Lara introduced the following invariant: the heterochromatic number of a  -graph
-graph  is the minimum number of colours
is the minimum number of colours  such that, in every colouring
such that, in every colouring ![$ \varsigma\colon V\to[c] $](/files/tex/598f01e1688f8608eceeeca230783e7c98fb24dc.png) there is an edge wich receives different colours in each of its vertices; that is, there exists
there is an edge wich receives different colours in each of its vertices; that is, there exists  such that
such that 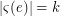 . If the heterochromatic number and the rank are equal, the hypergraph is said to be tight. Clearly a
. If the heterochromatic number and the rank are equal, the hypergraph is said to be tight. Clearly a 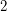 -graph is tight if and only if it is connected. A tight
-graph is tight if and only if it is connected. A tight  -forest is called a
-forest is called a  -tree.
-tree.
I can prove the following
 -forest has size
-forest has size 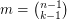 then it is tight — and therefore a
then it is tight — and therefore a  -tree.
-tree. Finally, we say that a  -forest is critical if no edge can be added to it without loosing the property of being a
-forest is critical if no edge can be added to it without loosing the property of being a  -forest; it is maximal (in size) with such a property. Observe that there are critical
-forest; it is maximal (in size) with such a property. Observe that there are critical  -forests of size
-forests of size  , whenever
, whenever 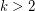 .
.
So, the conjecture is to motivate the question: ¿are critical  -forests tight?
-forests tight?
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
This has been solved.
See http://arxiv.org/abs/1109.3390