 login/create account
login/create account
Average diameter of a bounded cell of a simple arrangement
Conjecture The average diameter of a bounded cell of a simple arrangement defined by  hyperplanes in dimension
hyperplanes in dimension  is not greater than
is not greater than  .
.
 hyperplanes in dimension
hyperplanes in dimension  is not greater than
is not greater than  .
.
Let  be a simple arrangement formed by
be a simple arrangement formed by  hyperplanes in dimension
hyperplanes in dimension  . The number of bounded cells of
. The number of bounded cells of  is
is 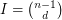 . Let
. Let 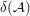 denote the average diameter of a bounded cell
denote the average diameter of a bounded cell 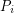 of
of  ; that is,
; that is, 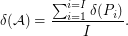 Let
Let  denote the largest possible average diameter of a bounded cell of a simple arrangement defined by
denote the largest possible average diameter of a bounded cell of a simple arrangement defined by  inequalities in dimension
inequalities in dimension  .
.
We have [DTZ,DX]:
If the conjecture of Hirsch holds, then 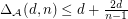 .
.
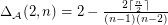 for
for 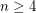 .
.
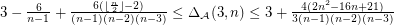 for
for 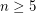 .
.
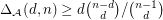 for
for 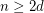 .
.
Bibliography
*[DTZ] A. Deza, T. Terlaky and Y. Zinchenko: Polytopes and arrangements : diameter and curvature. Operations Research Letters (to appear).
[DX] A. Deza and F. Xie: Hyperplane arrangements with large average diameter. Centre de Recherches Mathematiques and American Mathematical Society series (to appear).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University