Home » Subject » Graph Theory » Probabilistic G.T.

Chromatic number of random lifts of complete graphs

Importance: Medium ✭✭
Author(s): Amit, Linial, Matousek
Subject: Graph Theory
» Probabilistic Graph Theory
Keywords: random lifts, coloring
Recomm. for undergrads: no
Posted by: DOT
on: September 3rd, 2012
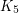Question   Is the chromatic number of a random lift of $ K_5 $ concentrated on a single value?

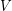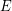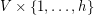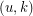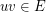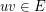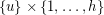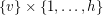Let $ G $ be a graph with vertex set $ V $ and edge set $ E $. An $ h $-lift $ H $ is a graph with vertex set $ V\times\{1,\dots,h\} $, such that $ (u,k) $ and $ (v,\ell) $ may only be adjacent in $ H $ if $ uv \in E $, and for each $ uv\in E $, the edges between $ \{u\}\times\{1,\dots,h\} $ and $ \{v\}\times\{1,\dots,h\} $ form a perfect matching.

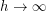A random $ h $-lift of $ G $ is a graph drawn uniformly at random from the set of all $ h $-lifts of $ G $. This amounts to choosing, independently at random, a perfect matching for each edge of $ G $. One is generally interested in properties of random $ h $-lifts when $ h\to\infty $.

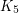Amit, Linial, and Matousek [ALM02] have studied the chromatic number of random lifts. They ask whether a the chromatic number of a random $ h $-lift of $ K_5 $ is asymptotically almost surely a single number.

It is easy to see that this number may be either 3 or 4. Farzad and Theis [FT12] have shown that random lifts of 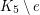$ K_5\setminus e $ are asymptotically almost surely 3-colorable.

A more general question is this.

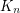Question   Is the chromatic number of a random lift of $ K_n $ concentrated on a single value?

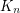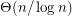Amit, Linial, and Matousek [ALM02] have shown that the chromatic number of a random lift of $ K_n $ is in $ \Theta(n/\log n) $.

Bibliography

*[ALM02] Random Lifts of Graphs III: Independence and Chromatic Number, A. Amit, N. Linial and J. Matousek, Random Structures and Algorithms, 20(2002) 1-22.

[FT12] Random lifts of 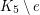$ K_5\setminus e $ are 3-colourable. B. Farzad and D.O. Theis. SIAM J. Discrete Math. 26:1 (2012), 169–179.


* indicates original appearance(s) of problem.
add new comment