 login/create account
login/create account
Concavity of van der Waerden numbers
For  and
and 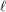 positive integers, the (mixed) van der Waerden number
positive integers, the (mixed) van der Waerden number 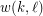 is the least positive integer
is the least positive integer  such that every (red-blue)-coloring of
such that every (red-blue)-coloring of ![$ [1,n] $](/files/tex/661d0acc09fbc5b62f49645a71cf7d831a26563f.png) admits either a
admits either a  -term red arithmetic progression or an
-term red arithmetic progression or an 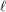 -term blue arithmetic progression.
-term blue arithmetic progression.
Conjecture For all  and
and 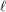 with
with 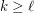 ,
, 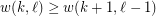 .
.
 and
and 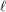 with
with 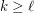 ,
, 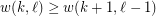 .
. The conjecture was stated in 2000 and published 2003 [LR] and 2007 [KL].
Bibliography
*[BL] Bruce Landman and Aaron Robertson, Ramsey Theory on the Integers, American Mathematical Society, Providence, Rhode Island, 2003.
[KL] Abdollah Khodkar and Bruce Landman, Recent progress in Ramsey theory on the integers, in Combinatorial Number Theory, 305-313, de Gruyter, Berlin, 2007.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University