 login/create account
login/create account
Cycle Double Covers Containing Predefined 2-Regular Subgraphs
Conjecture Let  be a
be a 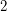 -connected cubic graph and let
-connected cubic graph and let  be a
be a 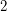 -regular subgraph such that
-regular subgraph such that 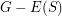 is connected. Then
is connected. Then  has a cycle double cover which contains
has a cycle double cover which contains  (i.e all cycles of
(i.e all cycles of  ).
).
 be a
be a 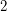 -connected cubic graph and let
-connected cubic graph and let  be a
be a 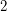 -regular subgraph such that
-regular subgraph such that 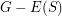 is connected. Then
is connected. Then  has a cycle double cover which contains
has a cycle double cover which contains  (i.e all cycles of
(i.e all cycles of  ).
). Used definitions in the above conjecture: a "cycle" is a connected 2-regular subgraph, a "cycle double cover" of a graph  is a set of cycles of
is a set of cycles of  such that every edge of
such that every edge of  is contained in precisely two cycles of the set. This conjecture has been motivated by Theorem 3, respectively, Theorem 4 in www.arxiv.org/abs/1711.10614. A weaker conjecture (Conjecture 14) has been stated in "Snarks with special spanning trees" (see www.arxiv.org/abs/1706.05595).
is contained in precisely two cycles of the set. This conjecture has been motivated by Theorem 3, respectively, Theorem 4 in www.arxiv.org/abs/1711.10614. A weaker conjecture (Conjecture 14) has been stated in "Snarks with special spanning trees" (see www.arxiv.org/abs/1706.05595).

 Drupal
Drupal CSI of Charles University
CSI of Charles University