 login/create account
login/create account
Decomposing the truncated octahedron into parallelepipeds (Solved)
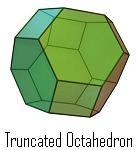
The motivation for this problem is a practical one. When sampling a set of points in 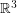 , it is convenient to use a lattice, and among lattices, it is best to choose one which is associated with a good sphere packing. Entezari, Dyer, and Moller [EDM] showed that some reconstruction problems associated with this type of data can be solved efficiently when the dual lattice has Voronoi cells which can be decomposed into parallelepipeds.
, it is convenient to use a lattice, and among lattices, it is best to choose one which is associated with a good sphere packing. Entezari, Dyer, and Moller [EDM] showed that some reconstruction problems associated with this type of data can be solved efficiently when the dual lattice has Voronoi cells which can be decomposed into parallelepipeds.
Two important dual lattices in 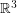 are the Face-Centered-Cubic lattice (FCC) and the Body-Centered-Cubic lattice (BCC) (see cubic lattices). The FCC lattice consists of all points in
are the Face-Centered-Cubic lattice (FCC) and the Body-Centered-Cubic lattice (BCC) (see cubic lattices). The FCC lattice consists of all points in  where the sum of the coordinates is even, and the BCC lattice consists of all points in
where the sum of the coordinates is even, and the BCC lattice consists of all points in 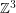 where all three coordinates have the same parity. The Voronoi cells of the FCC lattice are rhombic dodecahedra and the Voronoi cells of the BCC lattice are truncated octahedra. The rhombic dodecahedron can decomposed into parallelepipeds (this follows from the fact that this polyhedron is a projection of the 4-dimensional cube), and based on this Entezari, Dyer, and Moller found some practical sampling & reconstruction proceedures on the BCC lattice. However, as proved by Gauss (see [CG]), the FCC lattice has the densest sphere packing, so this lattice would be preferable for such applications were the Voronoi cells of its dual (truncated octahedra) decomposable into parallelepipeds.
where all three coordinates have the same parity. The Voronoi cells of the FCC lattice are rhombic dodecahedra and the Voronoi cells of the BCC lattice are truncated octahedra. The rhombic dodecahedron can decomposed into parallelepipeds (this follows from the fact that this polyhedron is a projection of the 4-dimensional cube), and based on this Entezari, Dyer, and Moller found some practical sampling & reconstruction proceedures on the BCC lattice. However, as proved by Gauss (see [CG]), the FCC lattice has the densest sphere packing, so this lattice would be preferable for such applications were the Voronoi cells of its dual (truncated octahedra) decomposable into parallelepipeds.
Solution
Thilo Roerig has pointed out that such a decomposition does exist and it follows from two well known facts. First, the truncated octahedron is a zonotope. Second, every zonotope has a decomposition into parallelipipeds. There is a 3D-model and an applet on a separate site.
Bibliography
[CG] J. H. Conway, N. J. A. Sloane, Sphere packings, lattices and groups. MathSciNet
[EDM] A. Entezari, R. Dyer, and T. Moller, Linear and Cubic Box Splines for the Body Centered Cubic Lattice
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University