Home » Subject » Geometry

Dirac's Conjecture

Importance: Medium ✭✭
Author(s): Dirac, Gabriel
Subject: Geometry
Keywords: point set
Recomm. for undergrads: no
Posted by: David Wood
on: January 22nd, 2014
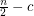Conjecture   For every set $ P $ of $ n $ points in the plane, not all collinear, there is a point in $ P $ contained in at least $ \frac{n}{2}-c $ lines determined by $ P $, for some constant $ c $.

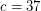In 1983, Beck[B], and independently Szemerédi and Trotter [ST], proved that for every set $ P $ of $ n $ points in the plane, not all collinear, there is a point in $ P $ contained in at least $ \frac{n}{c} $ lines determined by $ P $, for some large unspecified constant $ c $. Payne and Wood [PW] proved this result with $ c=37 $. Han [Han] improved this to $ c=3 $.

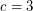Bibliography

[B] Jozsef Beck On the lattice property of the plane and some problems of Dirac, Motzkin and Erdős in combinatorial geometry. Combinatorica, 3(3-4):281–297, 1983.

*[D] Gabriel A. Dirac. Collinearity properties of sets of points. Quart. J. Math., Oxford Ser. (2), 2:221–227, 1951. MR: 0043485.

[PW] Michael S. Payne and David R. Wood. Progress on Dirac's Conjecture. Electronic J. Combinatorics 21.2:P2.12, 2014. arXiv:1207.3594.

[ST] Endre Szemerédi and William T. Trotter, Jr., Extremal problems in discrete geometry. Combinatorica 3.3-5:381-392, 1983.

[Han] Zeye Han. A Note on Weak Dirac Conjecture, Electronic J. Combinatorics 24.1:P1.63, 2017.


* indicates original appearance(s) of problem.
add new comment