 login/create account
login/create account
Direct product of reloids is a complete lattice homomorphism (Solved)
Conjecture If  is a filter object then
is a filter object then 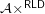 is a complete homomorphism of the lattice of filter objects to a complete sublattice of the lattice of reloids, if also
is a complete homomorphism of the lattice of filter objects to a complete sublattice of the lattice of reloids, if also 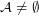 then it is an isomorphism.
then it is an isomorphism.
 is a filter object then
is a filter object then 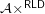 is a complete homomorphism of the lattice of filter objects to a complete sublattice of the lattice of reloids, if also
is a complete homomorphism of the lattice of filter objects to a complete sublattice of the lattice of reloids, if also 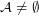 then it is an isomorphism.
then it is an isomorphism. See Algebraic General Topology for definitions of used concepts.
This conjecture is false. See example 14.5 (the number in the draft may change) in Algebraic General Topology book.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University