 login/create account
login/create account
Generalized path-connectedness in proximity spaces
Let  be a proximity.
be a proximity.
A set  is connected regarding
is connected regarding  iff
iff 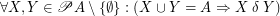 .
.
Conjecture The following statements are equivalent for every endofuncoid 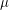 and a set
and a set 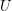 :
:
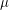 and a set
and a set 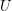 :
:- \item
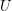 is connected regarding
is connected regarding 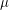 . \item For every
. \item For every 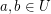 there exists a totally ordered set
there exists a totally ordered set 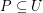 such that
such that 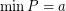 ,
, 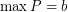 , and for every partion
, and for every partion 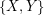 of
of 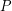 into two sets
into two sets 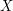 ,
, 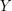 such that
such that 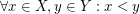 , we have
, we have ![$ X \mathrel{[ \mu]^{\ast}} Y $](/files/tex/0ef560be389646efd1fdde5ebc9afc9ac98ee64e.png) .
. Bibliography
*Question at math.StackExchange.com by Victor Porton
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
A proposed lemma
http://math.stackexchange.com/questions/691643/a-lemma-to-solve-a-conjec...
--
Victor Porton - http://www.mathematics21.org