login/create account
Hamiltonicity of Cayley graphs
Question Is every Cayley graph Hamiltonian?
This problem seems to have been first considered by Rapaport-Strasser [R]. Lovasz [L] conjectured more generally that every vertex-transitive graph is Hamiltonian. For a survey of results up to 1996, see [CG]. Although many specific Cayley graphs have been shown to be Hamiltonian, there are few general results. One exception is the theorem by Pak and Radoičić [PR] that every finite group 
with at least three elements has a generating set 
of size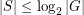 
, such that the corresponding Cayley graph is Hamiltonian.
Bibliography
[CG] S. J. Curran, J. A. Gallian, Hamiltonian cycles and paths in Cayley graphs and digraphs—a survey, Discrete Math. 156 (1996), 1–18.
[L] L. Lovasz, Problem 11, in “Combinatorial structures and their applications,” University of Calgary, Calgary, Alberta, Canada (1970), Gordon and Breach, New York.
[PR] I. Pak and R. Radoičić, Hamiltonian paths in Cayley graphs, preprint.
*[R] E. Rapaport-Strasser, Cayley color groups and Hamilton lines, Scripta Math. 24 (1959), 51–58.
* indicates original appearance(s) of problem.
[PR] paper
On September 21st, 2009 Anonymous says:
First, link to PR paper has moved with Pak homepage. Second, it is now published in Discrete Math.
Is this at all relevant?
On January 8th, 2009 Anonymous says:
Not sure but wondering if this link is at all relevant to the problem:
http://books.google.com/books?id=aSyXqtfOuU4C&pg=PA49&dq=Cayley+graph&num=100&client=firefox-a#PPA49,M1
Thanks,
- Farley
graphs vs. digraphs
On January 8th, 2009 md says:
The book you link to has examples of directed Cayley graphs with no (directed) Hamiltonian cycle. The existence of such graphs is interesting and relevant, but does not give a counterexample to the problem stated here.
Drupal
CSI of Charles University
Hamiltonicity of dence Cayley graphs
Christofides, Hladky, and Mathe (http://arxiv.org/abs/1008.2193) proved using the Regularity Method the case when the vertex-transitive graph is sufficiently dense.