 login/create account
login/create account
Inequality of the means
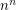 rectangular
rectangular  -dimensional boxes each of which has side lengths
-dimensional boxes each of which has side lengths 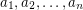 inside an
inside an  -dimensional cube with side length
-dimensional cube with side length 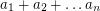 ?
? Taking the arithmetic/geometric mean inequality ![\[ (a_1 a_2 \ldots a_n)^{1/n} \le \frac{a_1 + a_2 + \ldots a_n}{n} \]](/files/tex/ddafd651e186a42dca67e3e09544ba4c8f91484f.png) multiplying both sides by
multiplying both sides by  and then raising both sides to the
and then raising both sides to the 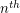 power yields:
power yields: ![\[ n^n \cdot a_1 a_2 \ldots a_n \le (a_1 + a_2 + \ldots a_n)^{n}.\]](/files/tex/89c7eac02bda8bfa0fa5b3e33b1dfc0836d8d96f.png) So, in the above question, the volume of the cube is at least the sum of the volumes of the rectangular boxes. Furthermore, a positive solution to this question would yield a strengthening of the arithmetic/geometric mean inequality.
So, in the above question, the volume of the cube is at least the sum of the volumes of the rectangular boxes. Furthermore, a positive solution to this question would yield a strengthening of the arithmetic/geometric mean inequality.
For 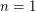 the problem is trivial, for
the problem is trivial, for  it is immediate, and for
it is immediate, and for 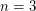 it is tricky, but possible. It is also known that a solution for dimensions
it is tricky, but possible. It is also known that a solution for dimensions  and
and  can be combined to yield a solution for dimension
can be combined to yield a solution for dimension 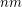 . Thus, the question has a positive answer whenever
. Thus, the question has a positive answer whenever  has the form
has the form 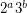 . It is open for all other values.
. It is open for all other values.
See Bar-Natan's page for more.
Bibliography
[BCG] E. R. Berlekamp, J. H. Conway and R. K. Guy, Winning Ways for Your Mathematical Plays, Academic Press, New York 1983.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University