 login/create account
login/create account
Jacob Palis Conjecture(Finitude of Attractors)(Dynamical Systems)
Conjecture Let  be the space of
be the space of 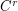 Diffeomorphisms on the connected , compact and boundaryles manifold M and
Diffeomorphisms on the connected , compact and boundaryles manifold M and 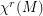 the space of
the space of 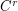 vector fields. There is a dense set
vector fields. There is a dense set  (
(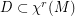 ) such that
) such that 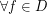 exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space
exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space 
 be the space of
be the space of 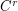 Diffeomorphisms on the connected , compact and boundaryles manifold M and
Diffeomorphisms on the connected , compact and boundaryles manifold M and 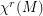 the space of
the space of 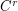 vector fields. There is a dense set
vector fields. There is a dense set  (
(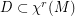 ) such that
) such that 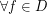 exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space
exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space 
This is a very Deep and Hard problem in Dynamical Systems . It present the dream of the dynamicist mathematicians .
Definition : A set  is an attractor for a Diffeomorphism (or a flow ) if it is invariant , transitive and the basin of attraction
is an attractor for a Diffeomorphism (or a flow ) if it is invariant , transitive and the basin of attraction 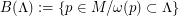 has positive Lebesgue Measure.
has positive Lebesgue Measure.
Bibliography
Bonatti C, Diaz L.; Viana M.; Dynamics beyond uniform hyperbolicity , Springer[Encyclopaedia of Mathematics Sciences ], Volume 102, 2005
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University