 login/create account
login/create account
KPZ Universality Conjecture
The KPZ equation is given by
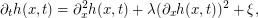
where 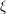 denotes space-time white noise and
denotes space-time white noise and 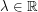 is a parameter describing the strength of its "asymmetry". It has been conjectured (see [BPRS93, BG97, Cor 12 ,GJ14,HQ18] for a number of results in this direction) that the KPZ equation has a “universal” character in the sense that any one-dimensional model of surface growth should converge to it provided that it has the following features:
is a parameter describing the strength of its "asymmetry". It has been conjectured (see [BPRS93, BG97, Cor 12 ,GJ14,HQ18] for a number of results in this direction) that the KPZ equation has a “universal” character in the sense that any one-dimensional model of surface growth should converge to it provided that it has the following features:
• There is a microscopic smoothing mechanism. Pictorially this means that large valleys are quickly filled.
• The system has microscopic fluctuations with short-range correlations. Pictorially this means that height function change depends only on neighboring heights.
• The system has some “lateral growth” mechanism in the sense that the growth speed depends in a nontrivial way on the slope. The vertical effective growth rate depends non-linearly on local slope.
• At the microscopic scale, the strengths of the growth and fluctuation mechanisms are well separated: either the growth mechanism dominates (intermediate disorder) or the fluctuations dominate (weak asymmetry). Growth is drive by noise which quickly decorrelates in space / time and is not heavy tailed.
Here is a concrete surface growth mathematical model to give a sense of the above features. The random deposition model is one of the simplest (and least realistic) models for a randomly growing one-dimensional interface. Unit blocks fall independently and in parallel from the sky above each site of  according to exponentially distributed waiting times. Recall that a random variable X has exponential distribution of rate
according to exponentially distributed waiting times. Recall that a random variable X has exponential distribution of rate 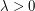 (or mean
(or mean 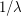 ) if
) if 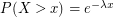 . Such random variables are characterized by the memoryless property – conditioned on the event that
. Such random variables are characterized by the memoryless property – conditioned on the event that 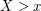 ,
, 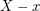 still has the exponential distribution of the same rate. Consequently, the random deposition model is Markov – its future evolution only depends on the present state (and not on its history). The ballistic deposition (or sticky block) model was introduced by Vold [V59] in 1959 and, as one expects in real growing interfaces, displays spatial correlation. As before, blocks fall according to iid exponential waiting times, however, now a block will stick to the first edge against which it becomes incident. This creates overhangs and we define the height function h(t, x) as the maximal height above x which is occupied by a box.
still has the exponential distribution of the same rate. Consequently, the random deposition model is Markov – its future evolution only depends on the present state (and not on its history). The ballistic deposition (or sticky block) model was introduced by Vold [V59] in 1959 and, as one expects in real growing interfaces, displays spatial correlation. As before, blocks fall according to iid exponential waiting times, however, now a block will stick to the first edge against which it becomes incident. This creates overhangs and we define the height function h(t, x) as the maximal height above x which is occupied by a box.
Bibliography
[BG97] L. BERTINI and G. GIACOMIN. Stochastic Burgers and KPZ equations from particle systems. Comm. Math. Phys. 183, no. 3, (1997), 571–607.
[BPRS93] L. BERTINI, E. PRESUTTI, B. RUDIGER ¨ , and E. SAADA. Dynamical fluctuations at the critical point: convergence to a nonlinear stochastic PDE. Teor. Veroyatnost. i Primenen. 38, no. 4, (1993), 689–741
[Cor 12] I. Corwin, The Kardar-Parisi-Zhang equation and universality class, Random Matrices Theory Appl. 1 (2012), 1130001, 76. MR 2930377. Zbl 1247.82040. http://dx.doi.org
[GJ14] P. GONC¸ ALVES and M. JARA. Nonlinear fluctuations of weakly asymmetric interacting particle systems. Arch. Ration. Mech. Anal. 212, no. 2, (2014), 597–644
[HQ18] HAIRER, M. and QUASTEL, J. (2018). A class of growth models rescaling to KPZ. Forum Math. Pi 6 e3
[V59] M. J. Vold. A numerical approach to the problem of sediment volume. J. Colloid Sci., 14:168 (1959).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University