 login/create account
login/create account
Monochromatic vertex colorings inherited from Perfect Matchings
 and
and  are there bi-colored graphs on
are there bi-colored graphs on  vertices and
vertices and  different colors with the property that all the
different colors with the property that all the  monochromatic colorings have unit weight, and every other coloring cancels out?
monochromatic colorings have unit weight, and every other coloring cancels out? Background: This and many related questions are directly inspired from quantum physics, and their solutions would directly contribute to new understanding in quantum physics.
Bi-Colored Graph: A bi-colored weighted graph 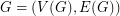 , on
, on  vertices with
vertices with  colors is an undirected, not necessarily simple graph where there is a fixed ordering of the vertices
colors is an undirected, not necessarily simple graph where there is a fixed ordering of the vertices 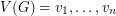 and to each edge
and to each edge 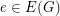 there is a complex weight
there is a complex weight 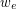 and an ordered pair of (not necessarily different) colors
and an ordered pair of (not necessarily different) colors 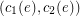 associated with it from the
associated with it from the  possible colors. We say that an edge is monochromatic if the associated pair of colors are not different, otherwise the edge is bi-chromatic. Moreover, if
possible colors. We say that an edge is monochromatic if the associated pair of colors are not different, otherwise the edge is bi-chromatic. Moreover, if  is an edge incident to the vertices
is an edge incident to the vertices 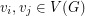 with
with 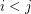 and the associated ordered pair of colors to
and the associated ordered pair of colors to  is
is 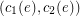 then we say that
then we say that  is colored
is colored 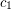 at
at 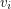 and
and 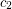 at
at 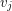 .
.
We will be interested in a special coloring of this graph:
Inherited Vertex Coloring: Let  be a bi-colored weighted graph and
be a bi-colored weighted graph and 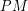 denote a perfect matching in
denote a perfect matching in  . We associate a coloring of the vertices of G with PM in the natural way: for every vertex
. We associate a coloring of the vertices of G with PM in the natural way: for every vertex 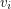 there is a single edge
there is a single edge 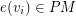 that is incident to
that is incident to 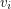 , let the color of
, let the color of 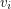 be the color of
be the color of 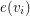 at
at 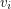 . We call this coloring
. We call this coloring  , the inherited vertex coloring (IVC) of the perfect matching PM.
, the inherited vertex coloring (IVC) of the perfect matching PM.
Now we are ready to define how constructive and destructive interference during an experiment is governed by perfect matchings of a bi-colored graph.
Weight of Vertex Coloring: Let  be a bi-colored weighted graph. Let
be a bi-colored weighted graph. Let 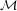 be the set of perfect matchings of
be the set of perfect matchings of  which have the coloring
which have the coloring  as their inherited vertex coloring. We define the weight of
as their inherited vertex coloring. We define the weight of  as
as 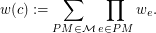 Moreover, if
Moreover, if 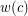 =1 we say that the coloring gets unit weight, and if
=1 we say that the coloring gets unit weight, and if 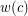 =0 we say that the coloring cancels out.
=0 we say that the coloring cancels out.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University