If 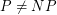, then 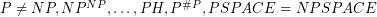, and a whole bunch more separations can be shown. In the light of this, if one believes that 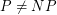, then it is naive to try to directly separate P from NP. In the words of the great George Polya, "If there is a problem you can’t solve, then there is an easier problem you can solve: find it." The P versus PSPACE question is one of the easiest such questions and would constitute an astonishing discovery in its own right. In particular, it would be the first separation result of this kind.

Problem Approaches

How do we approach this problem? I don't know, readers please contribute. My personal take would be circuit complexity, i.e. functions that are known not to be computable with circuits of polynomial size. Another would be descriptive complexity: show that there is a property that can be expressed in second-order logic with a transitive closure operation which cannot be recognized in polynomial time.[N87] Fenner offered an interesting characterization of the P versus PSPACE question in terms of reductions.[FKR89] P versus PSPACE was also as an intermediate step towards the P versus NP prize by the Clay institute.[F05]