 login/create account
login/create account
Partition of a cubic 3-connected graphs into paths of length 2.
Problem Does every 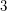 -connected cubic graph on
-connected cubic graph on 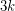 vertices admit a partition into
vertices admit a partition into  paths of length
paths of length 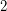 ?
?
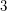 -connected cubic graph on
-connected cubic graph on 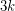 vertices admit a partition into
vertices admit a partition into  paths of length
paths of length 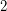 ?
? More generally, the following question is posed.
Problem Does every 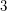 -connected cubic graph on at least
-connected cubic graph on at least 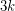 vertices contain
vertices contain  pairwise vertex-disjoint paths of length
pairwise vertex-disjoint paths of length 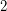 ?
?
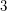 -connected cubic graph on at least
-connected cubic graph on at least 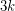 vertices contain
vertices contain  pairwise vertex-disjoint paths of length
pairwise vertex-disjoint paths of length 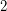 ?
? In [K1], Kelmans gave a construction that provided infi nitely many 2-connected graphs for which the above statement is false.
Bibliography
[K1] Alexander K. Kelmans, Packing 3-vertex paths in 2-connected graphs
*[K2] Alexander K. Kelmans, On 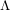 --Packing in 3--connected Graphs, RUTCOR Research Report 23--2005, Rutgers University. See also Packing 3-vertex Paths In Cubic 3-connected Graphs
--Packing in 3--connected Graphs, RUTCOR Research Report 23--2005, Rutgers University. See also Packing 3-vertex Paths In Cubic 3-connected Graphs
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University