Home » Subject » Combinatorics » Matroid Theory

Rota's unimodal conjecture

Importance: High ✭✭✭
Author(s): Rota, Gian-Carlo
Subject: Combinatorics
» Matroid Theory
Keywords: flat
log-concave
matroid
Recomm. for undergrads: no
Posted by: mdevos
on: June 8th, 2007

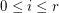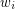Let $ M $ be a matroid of rank $ r $, and for $ 0 \le i \le r $ let $ w_i $ be the number of closed sets of rank $ i $.

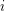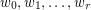Conjecture   $ w_0,w_1,\ldots,w_r $ is unimodal.
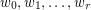Conjecture   $ w_0,w_1,\ldots,w_r $ is log-concave.

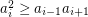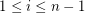A sequence $ a_0,a_1,\ldots a_n $ is log-concave if $ a_i^2 \ge a_{i-1} a_{i+1} $ for all $ 1 \le i \le n-1 $.

The first of these conjectures is due to Rota [R], the second is folklore as far as I (M. DeVos) know. The special case of proving the second conjecture for 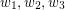$ w_1,w_2,w_3 $ amounts to showing that $ (\#lines)^2 \ge (\#points)(\#planes) $ and has been called the points-lines-planes conjecture. Seymour [S] proved this conjecture in the special case where every line contains at most four points, but it is still open in general.

Bibliography

*[R] Rota, Gian-Carlo, Combinatorial theory, old and new. Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 3, pp. 229--233. Gauthier-Villars, Paris, 1971. MathSciNet

[S] Seymour, P. D. On the points-lines-planes conjecture, J. Combin. Theory Ser. B 33 (1982), no. 1, 17--26. MathSciNet


* indicates original appearance(s) of problem.
add new comment