 login/create account
login/create account
The chromatic class of the cartesian product of graphs (Solved)
Conjecture Does there exist graphs  and
and  from Class 1 such that there Cartesian product is from Class 2?
from Class 1 such that there Cartesian product is from Class 2?
 and
and  from Class 1 such that there Cartesian product is from Class 2?
from Class 1 such that there Cartesian product is from Class 2? It is known that there are graphs  and
and  which are from Class 2 and their product is from Class 1. Our problem asks the symmetric question. Let us also note that from the classical result of A. Kotzig we imply that there are no regular graphs
which are from Class 2 and their product is from Class 1. Our problem asks the symmetric question. Let us also note that from the classical result of A. Kotzig we imply that there are no regular graphs  and
and  satisfying the conjecture.
satisfying the conjecture.
a more interesting result
On December 3rd, 2007 mdevos says:
a quick google search turned up the following theorem of Mahmoodian:
Theorem If 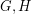 are graphs and
are graphs and  is class 1, then
is class 1, then  is class 1.
is class 1.
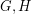 are graphs and
are graphs and  is class 1, then
is class 1, then  is class 1.
is class 1. the proof is not difficult and can be found here.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
trivially false
If and
and  are class 1, then
are class 1, then  is also class 1. Just choose a
is also class 1. Just choose a  -edge coloring of
-edge coloring of  and a
and a 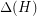 -edge coloring of
-edge coloring of  , and then assign each edge of
, and then assign each edge of  the color of the edge it projects to in the appropriate projection map. This gives a proper
the color of the edge it projects to in the appropriate projection map. This gives a proper  edge coloring of
edge coloring of  , and
, and 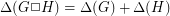 .
.