 login/create account
login/create account
The circular embedding conjecture
This conjecture implies the cycle double cover conjecture, since the list of cycles which bound faces covers each edge exactly twice. Let  be a cubic graph, let
be a cubic graph, let 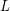 be a list of cycles covering every edge of
be a list of cycles covering every edge of  exactly two times, and form a topological space by gluing a disc to each circuit in
exactly two times, and form a topological space by gluing a disc to each circuit in 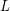 . This space is a surface, and every face is bounded by a cycle. Thus, the circular embedding conjecture and the cycle double cover conjecture are equivalent for cubic graphs. For general graphs, this construction may fail since the neighborhood of a vertex may not be a disc (it could be a pinchpoint).
. This space is a surface, and every face is bounded by a cycle. Thus, the circular embedding conjecture and the cycle double cover conjecture are equivalent for cubic graphs. For general graphs, this construction may fail since the neighborhood of a vertex may not be a disc (it could be a pinchpoint).
A stronger variant of this conjecture asserts that it is possible to find an embedding as above with the added condition that the dual graph is 5-colorable. This variant implies The five cycle double cover conjecture since the circuits bounding faces of a given color class may be grouped into a cycle. Next we state a different strengthening which asserts that we may find an embedding as above into an orientable surface.
If this conjecture is true, then the oriented cycle double cover conjecture (see cycle double cover) is also true, since the list of circuits bounding faces all traversed in the clockwise direction cover each edge exactly once in each direction (since the surface is orientable, we may specify a global clockwise orientation). As was the case above, the oriented circular embedding conjecture is equivalent to the oriented cycle double cover conjecture for cubic graphs. Also as above, there is a strengthening of this conjecture which asserts that the graph may be embedded so that the dual graph is 5-colorable. If true, this would imply The orientable five cycle double cover conjecture.
Bibliography
[H] G. Haggard, Edmonds characterization of disc embeddings. Proceedings of the Eighth Southeastern Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1977), pp. 291--302. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University