 login/create account
login/create account
Bentz, Cedric
Finding k-edge-outerplanar graph embeddings ★★
Author(s): Bentz
Conjecture It has been shown that a  -outerplanar embedding for which
-outerplanar embedding for which  is minimal can be found in polynomial time. Does a similar result hold for
is minimal can be found in polynomial time. Does a similar result hold for  -edge-outerplanar graphs?
-edge-outerplanar graphs?
 -outerplanar embedding for which
-outerplanar embedding for which  is minimal can be found in polynomial time. Does a similar result hold for
is minimal can be found in polynomial time. Does a similar result hold for  -edge-outerplanar graphs?
-edge-outerplanar graphs? Keywords: planar graph; polynomial algorithm
Approximation ratio for k-outerplanar graphs ★★
Author(s): Bentz
Conjecture Is the approximation ratio for the Maximum Edge Disjoint Paths (MaxEDP) or the Maximum Integer Multiflow problem (MaxIMF) bounded by a constant in  -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs?
 -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs? Keywords: approximation algorithms; planar graph; polynomial algorithm
Approximation Ratio for Maximum Edge Disjoint Paths problem ★★
Author(s): Bentz
Conjecture Can the approximation ratio 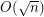 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 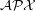 -hardness?
-hardness?
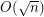 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 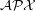 -hardness?
-hardness? Keywords: approximation algorithms; Disjoint paths; planar graph; polynomial algorithm

 Drupal
Drupal CSI of Charles University
CSI of Charles University