 login/create account
login/create account
density problems
Sidorenko's Conjecture ★★★
Author(s): Sidorenko
Conjecture For any bipartite graph  and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 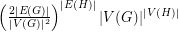 .
.
 and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 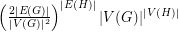 .
. Keywords: density problems; extremal combinatorics; homomorphism

 Drupal
Drupal CSI of Charles University
CSI of Charles University