 login/create account
login/create account
knot space
Realisation problem for the space of knots in the 3-sphere ★★
Author(s): Budney
Problem Given a link  in
in 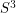 , let the symmetry group of
, let the symmetry group of  be denoted
be denoted 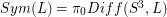 ie: isotopy classes of diffeomorphisms of
ie: isotopy classes of diffeomorphisms of 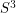 which preserve
which preserve  , where the isotopies are also required to preserve
, where the isotopies are also required to preserve  .
.
 in
in 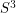 , let the symmetry group of
, let the symmetry group of  be denoted
be denoted 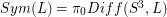 ie: isotopy classes of diffeomorphisms of
ie: isotopy classes of diffeomorphisms of 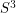 which preserve
which preserve  , where the isotopies are also required to preserve
, where the isotopies are also required to preserve  .
.
Now let  be a hyperbolic link. Assume
be a hyperbolic link. Assume  has the further `Brunnian' property that there exists a component
has the further `Brunnian' property that there exists a component 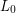 of
of  such that
such that  is the unlink. Let
is the unlink. Let 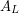 be the subgroup of
be the subgroup of 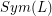 consisting of diffeomorphisms of
consisting of diffeomorphisms of 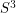 which preserve
which preserve 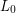 together with its orientation, and which preserve the orientation of
together with its orientation, and which preserve the orientation of 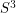 .
.
There is a representation 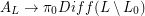 given by restricting the diffeomorphism to the
given by restricting the diffeomorphism to the  . It's known that
. It's known that 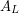 is always a cyclic group. And
is always a cyclic group. And 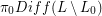 is a signed symmetric group -- the wreath product of a symmetric group with
is a signed symmetric group -- the wreath product of a symmetric group with 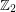 .
.
Problem: What representations can be obtained?
Keywords: knot space; symmetry

 Drupal
Drupal CSI of Charles University
CSI of Charles University